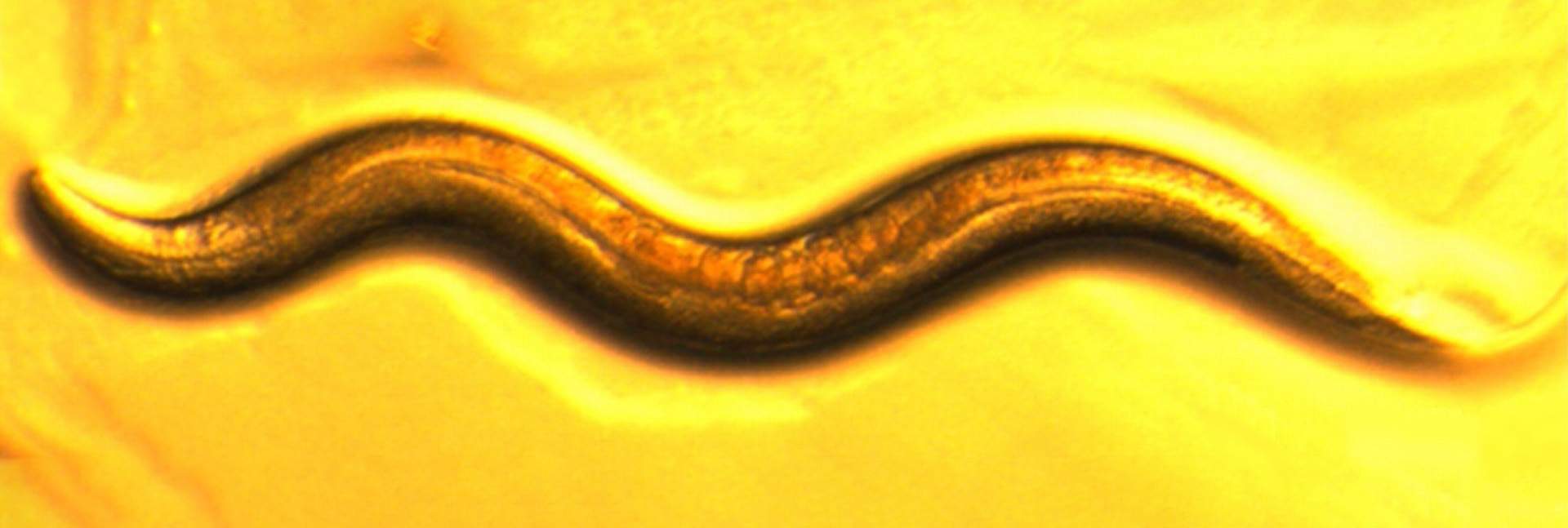
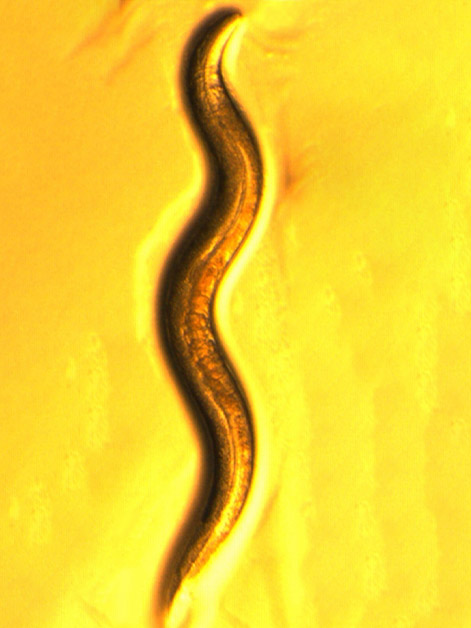
The throat of the roundworm Caenorhabditis elegans might seem like an odd place for exploring the complexity of life’s mechanisms, until one realizes how much information has been collected on these tiny nematodes over the past several decades. This wealth of data was a major reason the worm was chosen as the focus of a new Weizmann Institute of Science study that shows the power of mathematical and algorithmic models in allowing for fine-grained, high-resolution understanding of biological systems.
In the study, Dr. Dana Sherman and Prof. David Harel of Weizmann’s Computer Science and Applied Mathematics Department constructed a mathematical model of the behavior of the nematode’s feeding organ, the pharynx, in order to simulate and analyze in exacting detail the way in which its swallowing motions are generated. Beyond shedding new light on the dynamics of this process, the study demonstrates how computer simulations can, within minutes, help conduct biological experiments that would have taken years in the lab, were they even feasible.

A model superstar
With a transparent body and roughly only 1,000 cells, C. elegans is a scientific superstar that has facilitated groundbreaking discoveries in biology, including several leading to Nobel Prizes. Its genome was the first to be fully sequenced among multicellular organisms, enabling detailed genetic studies, and its physique is ideal for real-time observation of biological processes. Scientists have also mapped its entire neuronal wiring diagram and cell lineage. To top it all off, C. elegans shares many biological pathways with humans, making it an excellent model for understanding fundamental processes such as aging, neurobiology and cell differentiation.
“"Computer scientists are used to building models that prepare us for the building of the real thing – say, planes or pacemakers. Our model aims to explain the behavior of an existing system"
The worm’s pharynx, a muscular organ composed of several dozen cells, goes through pumping motions that result in the intake of food particles from the environment. In the new study, Sherman and Harel resorted to classical mathematics to build a model of the pumping, using a bottom-up approach – that is, starting from the basic components to reconstruct a larger system. These components and parameters included data on, among other things, various types of throat muscle cells, neurons that send signals to the muscles, the propagation of these signals and the concentrations of different ions in the muscle cells. The model also included a description of the flow of fluids and food particles through the worm’s throat.

One might ask, however: Why build a model of something that’s already been built by nature?
“Computer scientists are used to building models that prepare us for the building of the real thing – say, planes or pacemakers,” Harel says. “In contrast, our model aims to explain the behavior of an existing, complex biological system. If you manage to construct a model whose behavior matches everything that’s known about the system, you can then run this model under different conditions, potentially observing unknown phenomena. This paves the way for lab experiments, which can then corroborate or refute the model’s predictions.”
Harel further explains that when a biological system is being modeled, simulated manipulations of its genes or cells must produce results that match what’s already known about this system from real life. Or, as he puts it, “If you are trying to model the development of a pancreas, you shouldn’t end up with something that looks like a pinky finger.”

Pumping up the system
The result of six years of research, the new Weizmann Institute model comprises a comprehensive description of the mechanisms that generate motion in different areas of the worm’s pharynx, making it possible to carry out quantitative analyses of the pharynx as a whole, as well as of its various components. As a result, the model provides a detailed explanation of how the pharynx works – something that had not been properly attempted before.
For example, it was known that the contractions and relaxations that make up the pharynx’s pumping motions are not perfectly synchronized: The contractions start at different points in time in various parts of the throat, spreading through these parts at different speeds. However, it was also known that the neural signals that initiate pharyngeal contractions spread very rapidly, almost simultaneously throughout the organ. If the contractions tightly followed those neural signals, they should have occurred in a nearly synchronized manner. The model was able to suggest a mechanism for explaining those apparently contradictory dynamics.

Moreover, the model provided a previously unavailable quantitative assessment of many parameters and explained at a fine resolution the interplay between the various muscles, both within each area of the throat and between different areas. Other analyses suggested that cells located on the throat’s margins play a role in its function and not only its structure, as is currently assumed. In addition, the model predicted that in tiny organisms such as C. elegans, the generation of a long-lasting electrical signal, such as the one generated within the pharyngeal muscles, must involve ions other than calcium.
Finally, the scientists used their model to conduct experiments by means of computer simulations, referred to as “in silico,” an allusion to the in vitro and in vivo experiments common in biology. The researchers employed such simulations to test, for example, how changes in the size or geometrical shape of the throat would affect the flow of particles during swallowing. Aside from their nearly instant execution, such in silico experiments demonstrate another advantage of mathematical models: They enable arbitrary manipulations, even those that are infeasible in the lab.