Are you a journalist? Please sign up here for our press releases
Subscribe to our monthly newsletter:
Share
Many of us in the modern world spend a good part of our day viewing 2-D representations of the 3-D world: drawings and photos, television and electronic screens, to name a few. Our brains automatically translate what we see into three dimensions. Not just that, but we unthinkingly group objects together, identify people from their photos no matter how they are posed, and gauge distances between objects. To the average computer, however, images are basically collections of colored dots in a 2-D grid. One of the bigger challenges for today’s computer scientists is to get these machines to relate to the 3-D world portrayed in their 2-D files as humans do – by sorting, classifying, comparing and inferring.
Dr. Yaron Lipman, who joined the Weizmann Institute’s Computer Science and Applied Mathematics Department in 2011, deals with the mathematics of deformation – variations in shape between similar objects or in that of a single body as it turns, twists, stretches or bends. His work has implications for fields as far-ranging as biology and computer-generated animation, engineering and computer vision.
One of the more basic questions is: In a group of objects, how does one decide whether any two are the same or different? This is not a trivial question, even for humans: To the untrained eye, for example, a pile of old animal bones may be a collection of similar objects, but a trained morphologist or paleontologist will be able to sort them into different species. That ability often comes with years of practice and, just as the average person can tell a pear from an apple without much thought, the expert can distinguish between bones without consciously tracing each step leading up to a particular identification. How, then, does one translate this type of thinking, which is at least partly unconscious, to a mathematical computer algorithm?
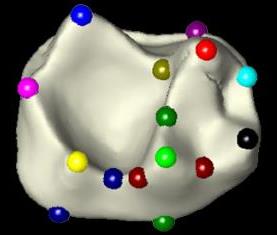
Lipman and his colleagues developed an algorithm for comparing and classifying anatomical surfaces such as bones and teeth by analyzing plausible deformations among their three-dimensional models. While a human working from a subjective point of view might look for identifying “landmarks” – for example a specific type of recognizable ridge or protrusion – the computer would take a different track: matching the surfaces globally while minimizing the amount of distortion in the match. A human often works from the bottom up, looking for local cues and then putting them together to arrive at a conclusion. In contrast, the algorithm is designed to consider the collective surfaces as a geometric whole and match them in a top-down manner. Lipman then gave his algorithm the ultimate test – pitting its bone and tooth identification against that of expert morphologists. In all the tests, the computer performed nearly as well as the trained morphologists. That means, he says, that non-experts could use the algorithm to quickly obtain accurate species identification from bones and teeth. In the future, further biological information might be more easily extracted from shape.
A second line of research in Lipman’s group is the distantly related problem of image matching. In recent years, as digital cameras are found in every pocket and purse, vast numbers of images are recorded and uploaded to visual media every day. This makes one of the great challenges of computer vision — the ability to interpret, analyze and compare image content automatically – more pressing than ever. In contrast to surfaces, images contain many local cues and features that are easy for a human brain to grasp for recognition. A computer, however, would assign all the points in the image equal importance. So a pair of photos taken with different lighting or from different angles, which a human would have no trouble identifying as the same person, might confound a computer’s point-matching algorithm. Lipman’s solution is to introduce an algorithm for distortion – that is, to determine a mathematical distortion limit on the ways that one set of points can morph into a second set. Somewhat surprisingly, this technique eliminates most of the false matches.
Yet another train of investigation Lipman pursues is that of modeling mappings and deformations, in 3-D space, of objects that possess desired geometric properties. This area is relevant to computer-generated animation, whose practitioners are constantly in search of better methods for creating life-like motion on screen; engineering, in which computerized models of objects are deformed and mapped to each other; and such areas as medical imaging and computer modeling. Such mappings are laid out on top of a representation of the object as a sort of 3-D mesh of tetrahedrons, and they are then used to work out how the various parts of the mesh deform as the object moves. In real life, this movement involves many parameters, including flexibility, elasticity, movement patterns of joints and the sites where surfaces meet. Lipman develops particular models of deformations that are able to avoid high distortion and self-penetration of matter — both properties of great importance for modeling deformations in “real-life” applications.
Dr. Yaron Lipman's research is supported by the Friends of Weizmann Institute in memory of Richard Kronstein
Share
