עלי שלכת נושרים לאט
ורוח ערב לוחש בלאט
לך נערה זו מנגינה של סתיו.
("ליל סתיו" מאת חיה כהן וחיים צור)
ניסוי מדעי 'נכון' הוא אלגנטי,פשוט וחסר שימוש". כך סבר פרופ' אלישע מוזס מהמחלקה לפיסיקה של מערכות מורכבות במכון ויצמן למדע במשך שנים רבות. פרופ' מוזס חוקר תופעות המתחוללות במערכות דינאמיות, המשתנות ו/או מתפתחות עם הזמן. למשל, קרומים(ממברנות) שמשנים את צורתם. למשל,תאחי שנע בתוך מערכת ביולוגית הכוללת כמה אלפי תאים חיים. למשל, להבת אש שמתפתחת ושורפת שכבה דקה של חומר כלשהו.
בדרך כלל מכוונים מחקריו של פרופ' מוזס להבנת אורחו ורבעו של הטבע.יישומים טכנולוגיים עולים מתוך המחקרים האלה,כאפשרויות עתידיות רחוקות למדי.אבל לא כך קרה למחקר שהתחיל בשנת1995,כאשר חגי אייזנברג, אז תלמיד מחקר לתואר שני במדרשת פיינברג, פסע אל תוך מעבדתו של מוזס כשהוא אוחז בידו דף נייר.אל מול מבטו המופתע של מוזס שמט התלמיד את הנייר שהתעופף במסלול "זיג-זג" עד שנחת על רצפת המעבדה. "את התופעה הזאת", אמר חגי, "אני רוצה לחקור". מוזס "נדלק" מיד.זו נראתה לו שאלה אלגנטית,פשוטה וחסרת יישום קרוב, בדיוק כמו שמחקר מדעי אמור להיות.
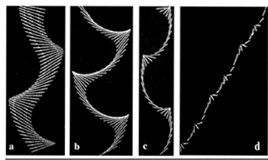
הבעיה הזאת (כיצד נופלים עצמים לא כדוריים בתוך נוזל או גז), היוותה אתגר מתמשך בשביל הפיסיקאים שעסקו בחקר המכניקה של נוזלים במשך 150 השנים האחרונות. ג'יימס מקסוול ולורד קלווין ניסו לשווא להציע משוואות שינבאו בדייקנות את דרכם ואת מסלול נפילתם של עצמים כאלה. אבל ההיסטוריה הזאת לא ריפתה את ידיהם של מוזס ואייזנברג. הם החליטו לחזור ולהסתער על האתגר הוותיק הזה, ולשם כך בנו, יחד עם אנדרו בלמונטה, מכל דק מאוד מזכוכית.אחר כך מילאו אותו במים והפילו אל תוכו רדידי מתכת. תצפיות מדוקדקות על המערכת הדו-ממדית הזאת הובילו את המדענים לניסוח מודל תיאורטי שניבא במידה רבה של דיוק את מסלולו של עלה מתכת מראש המכל אל תחתיתו. מודל דו-ממדי זה ניתן להרחבה מסוימת, כך שיוכל לשמש לתיאור תופעת נפילתם של עלי שלכת,או גופים אחרים, במערכת תלת-ממדית.
כללית, החוקרים מצאו שני אופני תנועה: תנודה מצד לצד תוך כדי נפילה, או גלגול תוך נפילה לצד אחד. הם גם גילו שקיימת מידה (המכונה מספר FROUDE) הקובעת את סוג התנועה שתתחולל. ידוע שמספר זה קובע גם את התקדמותם של כלי שיט על המים, וכן את קצב הליכתם של בעלי חיים, כלומר,מתיהם עוברים מהליכה לריצה וכו'. מספר FROUDE כולל יחס מסוים בין גודל העלה הנופל לבין משקלו. כך, עלה ארוך יותר יתנדנד, ואילו עלה כבד יותר - יתגלגל.בתהליך פיתוח המודל השתמשו החוקרים בכלים שמקורם בתורת הכאוס המתמטית (המבוססת על התפתחות של הבדלים זעירים בתנאי הפתיחה של התהליך הנחקר). אבל,בתצפיות שביצעו במערכת הניסוי שבנו לא נמצאה התנהגות כאוטית של העלים הנופלים.
המודל המתמטי הזה תואר בכמה כתבי עת מדעיים מכובדים, ובדרך הטבע, מוזס כבר שקע במחקר הבא שלו, הקשור לדרך תנועתם של תאים חיים. אבל העצמים הלא-כדוריים הנופלים סירבו לצאת מחייו. הדרך שבה דף נייר גולש ומרפרף אל הקרקע דומה לדרך שבה עלה מתכת נופל אל קרקעיתו של מכל מים, ודומה לדרך שבה שוקעת צוללת פגועה –כמו הצוללת הרוסית "קורסק" שטבעה לפני כשנה וחצי בים הצפוני, וכמו ה"דקר" הישראלית שאבדה בשנת1969ונמצאה לאחר שנים על קרקע הים בסמוך לאי כרתים. מוזס ואייזנברג,שהיו ערים לדמיון הזה,הציעו לסייע למחפשי ה"דקר" בהבנת מסלול נפילתה של הצוללת אל קרקע הים. שימוש במודל המתמטי שלהם,בצירוף ניסיונות שבוצעו בשיתוף עם חיל הים הישראלי במערכת תלת-ממדית, אכן הוביל להשגת תובנות באשר לאסון ה"דקר".
"טוב לראות כיצד מחקר תיאורטי לחלוטין עשוי להפוך - בלי שום רמז מוקדם –לרלוונטי לעניינים כל כך מעשיים וחומריים" ,אומר פרופ' מוזס. "נראה שבסופו של דבר,מחקר מדעי 'נכון' אכן חושף משהו מתכונות הטבע,ובכך הוא עשוי ביום מן הימים להציע סיוע חשוב וייחודי".