Are you a journalist? Please sign up here for our press releases
Subscribe to our monthly newsletter:

The year was 1815. Napoleon Bonaparte had just been defeated at Waterloo and Sadi Carnot, a young officer in his army, was being returned to Paris at a quarter of his former pay. Sadi’s transgression was actually that of his father, Lazare Carnot, who had been Napoleon’s interior minister and thus his minister of war during the infamous “Hundred Days.” Lazare and Sadi Carnot, were French army officers, but they were both also accomplished mathematicians and engineers.
Steam engines were just coming into use, and the English steam engine was much more efficient than everyone else’s, giving them a significant military advantage. Carnot, who remained a patriot despite his demotion, believed that French steam engines could be improved to beat the English ones. After researching the basic physics and mechanics of steam engines, he sent papers reporting his work to scientific journals. But he did not succeed in getting them published, and he ended up self-publishing a book from his own meager funds that he called Reflections on the Motive Power of Fire.
In his reflections on steam engines – in essence the conversion of heat to work – Carnot had achieved a crucial insight into the efficiency of this process, which he expressed in a formula for understanding the efficiency limit -- that is, the maximal amount of work that can be produced from the available heat.
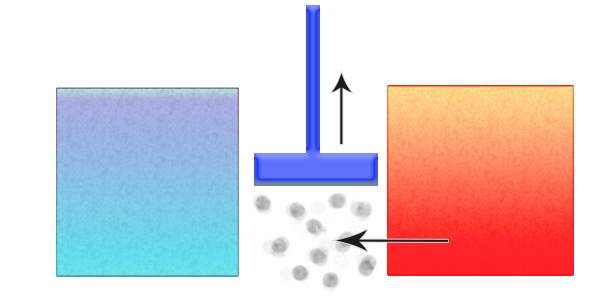
The ideal heat engine
Spoiler alert: Today, 194 years after Carnot published his book, his principles and the limits he proposed still hold true. And they are true for a field of physics that was nowhere near existence in his day – that of quantum mechanics.

Carnot wrote of an “ideal heat engine” that was made up of two “reservoirs” – one hot and one cold -- a working fluid, and a piston that converts the heat energy to motion. This, in principle, is the basis of the combustion engine.
Some 20 years after Carnot published his Reflections, they were revisited by another officer, Rudolf Clausius, who was in the Prussian cavalry. William Thomson, better known as Lord Kelvin, examined them as well. These two found that the upper limit that could exist in theory for the efficiency of any heat engine is the limit that Carnot had set. This limit, they concluded, corresponds to a heat engine that produces no entropy in a cycle of its operation. Entropy is universal – it is measured by the number of states in which a system can exist. Or, to put it simply, entropy is the amount of disorder in a system.
Clausius and Lord Kelvin showed that Carnot’s limit to efficiency follows from the second law of thermodynamics, which says that entropy can only remain constant (which corresponds to Carnot’s limit) or increase. Had there been a way to make entropy decrease it would have signified the reversal of the sense of time (“the time’s arrow problem”). The Carnot limit has since been elevated to the rank of a basic law of nature.
Does Carnot’s limit apply to atoms and electrons?
Many more decades passed before John von Neumann showed that the laws of thermodynamics apply also to the realm of quantum mechanics − which was surprising, since this is a world in which many other laws of classical physics do not apply.
Then, in 2003, Marlan Scully at Texas A&M proposed a way around Carnot’s limit. His proposal involved “quantum fuel” in which the energy levels (states) of electrons in atoms were changed by two lasers, making these states “coherently” interfere with each other in a fashion determined by the phases of the lasers (similar to the phases of electric currents). Scully showed that the temperature of the heat reservoir could be raised by choosing suitable phases for the lasers. This phase-dependent increase in the difference between the temperatures of the hot and cold reservoirs was shown to raise the efficiency of the system above the limit fixed by Carnot, much to everyone’s surprise.
In recent years, the German physicist Eric Lutz has proposed raising the temperature of the hot reservoir in another way, through so-called “quantum squeezing” − an operation that changes the noise that accompanies the quantum radiation in the reservoir in a fashion that depends on the phase of this radiation.
Heat, work and quantum engines

Fast forward to the present day: Prof. Gerson Kurizki and members of his group, postdoctoral fellows Drs. Wolfgang Niedenzu, Victor Mukherjee and Arnab Ghosh in the Weizmann Institute of Science’s Chemical and Biological Physics Department, revisited these reported differences between standard (“classical”) and quantum heat engines. They showed, in a paper recently published by Nature Communications, that it is crucial to carefully distinguish between heat and work supplied by the reservoir to the quantum engine. They concluded from this distinction that an engine fueled by a squeezed reservoir was not purely a heat engine, since some work was put into the engine by the quantum squeezing of the reservoir. This made it a sort of hybrid machine in which extra work was added to the heat, so that the “rules of the game” defined by Carnot and his followers for strict heat-to-work conversion did not apply. This was the reason the Lutz machine could surpass the Carnot efficiency limit. The Scully machine, by contrast, was found by Kurizki and his group to be a bona-fide heat engine, except that Scully’s quantum fuel raises the amount of heat provided to the engine, so that it meets the conditions set by Carnot.
Squeezing the piston
There is however an alternative route that adheres to Carnot’s rules and yet endows the engine with a “quantum advantage.” Kurizki’s group, together with Prof. Luiz Davidovich of Brazil, showed, in a paper published by the Proceedings of the National Academy of Science (PNAS), that instead of “squeezing” the reservoir, one can “squeeze” the noise of a quantum device which plays the role of a piston that extracts work from the engine. Such squeezing of the piston, they found, should strongly increase the work and power output of the engine. But – and this is a significant but – the increase still does not surpass Carnot’s limit. This is because its effect, which they called “quantum catalysis,” accounts for the “cost” of the work that had to be invested in squeezing the piston. Yet it still resulted in an increased amount of heat converted into work output.
Carnot died at age 36, eight years after the book was published. Forced to relinquish his army post with no pension, he died of cholera in the mental institution where he had been hospitalized for the last few years of his life. He could not have imagined that his findings would turn out to be relevant 194 years after he self-published them. Even less could he have imagined their relevance to engines that are as far as one can get one can get from the steam engines of his day and still be called a heat engine.
Prof. Gershon Kurizki's research is supported by Dana and Yossie Hollander. Prof. Kurizki is the incumbent of the George W. Dunne Professorial Chair of Chemical Physics.