The Notorious Piston and Other Problems

Haste makes waste, but we do need to get a move on. In life, as in physics, fast and slow can clash – or they can even out. When light, fast-moving particles are put into a box and mixed with heavy, slow-moving ones, they tend to collide with one another over and over. One of the underlying assumptions of the field of statistical mechanics is that such collisions transfer energy between the particles until the system reaches, on average, an energy equilibrium. But this basic physical rule has some puzzling exceptions. A new study, which was recently reported in the Proceedings of the National Academy of Sciences, PNAS, suggests a way to overcome a main mechanism that, in certain cases, accounts for the lengthy delay in the time it takes such systems to reach equilibrium.  

Prof. Vered Rom-Kedar of the Weizmann Institute of Science’s Computer Science and Applied Mathematics Department explains that it is actually quite difficult to transfer energy efficiently between fast- and slow-moving bodies. One can imagine atoms of gas in a container – or on a “billiard table,” as it is described in her area of mathematics. These atoms are moving fast, and they collide with each other and with the table walls. Now imagine that one of the table’s walls is springy – a sort of heavy shelf attached to a spring. If we observe this system for some time, we will see that the temperature of the gas (which corresponds to the average of the kinetic energy of the atoms) will appear to go up and down periodically. This means that the energy of the shelf and the gas will not equilibrate for a long time. The lighter the particles, the longer this periodic behavior will continue.

The “notorious piston problem” defies the very basic assumption of statistical equilibrium on which the field of statistical mechanics relies

The key feature of this particular billiard system is that for any fixed shelf position the movement of the fast particles is chaotic. The chaotic nature of the motion means that one can’t predict the exact behavior of a particular atom. Yet such chaotic behavior implies that the motion is ergodic – a mathematical term that describes a system in which the average energy of a particle over long periods of time is the same as its averaged energy over all its possible configurations within the system. In other words, when a system is ergodic, one can estimate the particles’ averaged effect on the springy wall. So if we perform this averaging, we will conclude that the energy of the wall changes periodically, on average, on time scales that can be estimated using the ratio between the shelf and the particles’ masses.

The behavior of slow-fast systems that do not reach equilibration on long time scales was first observed in a similar theoretical problem in which a gas is placed in two chambers that are separated by a heavy piston, and the system is initially out of equilibrium. This old problem, known as the “notorious piston problem,” defies the very basic assumption of statistical equilibrium on which the field of statistical mechanics relies.

Time to equilbrium

Rom-Kedar and her colleagues, Prof. Kushal Shah of the Indian Institute of Science Education and Research, Bhopal India; Prof. Dmitry Turaev of Imperial College, London; and Prof. Vassili Gelfreich of the University of Warwick, Coventry, UK, decided to dig deeper into this phenomenon using billiards models. In their models, a fast moving particle on a billiards table with one springy wall bounces off the wall according to the usual mechanical laws of elastic collisions, so the particle and the springy wall change their speeds when they collide.

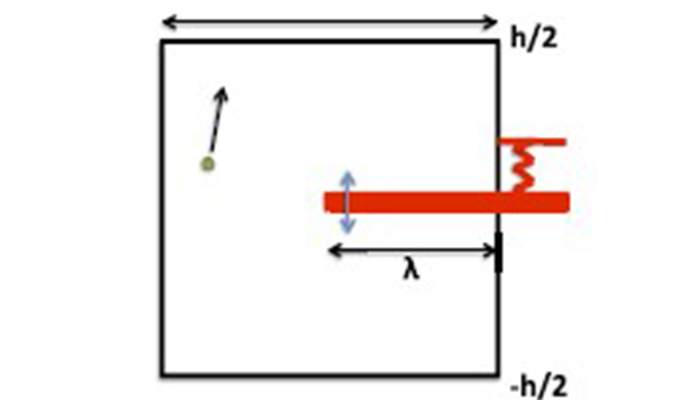
Looking at different billiard tables, the researchers showed that the transfer of energy between a particle and the springy wall or piston can be accelerated a great deal if the particles have the “freedom of choice,” once in a while, to be in one part of the box or another. In this case, the dynamics of the particle for some fixed position of the springy walls is not ergodic. If, for example, the springy part forms a shelf in a rectangular container and the particle can “choose” to go either under or over the shelf, the transfer of energy becomes very efficient. They showed that the system as a whole equilibrates in a finite amount of time, even when the ratio between the mass of the particle and that of the shelf approaches zero.

This equilibration process, according to their further research, is similar to that achieved in a specific random system that they defined, which is independent of the particle-shelf mass ratios. Other boxes and tables in which the particles can “choose” to spend some time without coming into contact with the springy wall were also shown to behave in a similar manner. 

In short, these results demonstrate that a lack of ergodicity in the fast particles dynamics can greatly accelerate the ergodicity of the system as a whole. This surprising, counter-intuitive conclusion may help explain numerous real-life physical systems in which the speeds of the different components are on different scales, separated by orders of magnitude; and it provides new insight into one of the long-standing open questions in statistical mechanics. 

Prof. Vered Rom-Kedar is the incumbent of the Estrin Family Professorial Chair of Computer Science and Applied Mathematics.