Are you a journalist? Please sign up here for our press releases
Subscribe to our monthly newsletter:
Share
The story begins in two separate locations in the Institute’s physics buildings. In one of those – the lab of Prof. Yaron Silberberg – research students Yoav Lahini and Mor Verbin were experimenting with a quasicrystalline optical system. Quasicrystals, discovered 30 years ago by Prof. Dan Schechtman of the Technion, are unique in the arrangement of their atoms: Like regular crystals, they are arranged in an orderly fashion but, unlike most crystals, that arrangement is not periodic. Quasicrystals represent a new type of matter; recognition of this fact changed the face of materials science and forced scientists to redefine the meaning of the term “crystal.” Schechtman received the 2011 Nobel Prize in Chemistry for his discovery, which garnered interest among crystallographers, chemists, physicists and mathematicians alike. Yoav and Mor, who were studying a new type of optical quasicrystals developed in the lab, had noticed some strange, inexplicable phenomena taking place at their crystals’ edges. They measured, but could not explain, these phenomena.
In another part of the physics buildings, research students Oded Zilberberg in the group of Prof. Yuval Gefen, Yaacov Kraus in the group of Prof. Adi Stern and Zohar Ringel in the group of Prof. Ehud Altman were becoming interested in the new field of topological materials. These materials, discovered in 2007, are mostly normal, periodic crystals, but they have unusual electrical properties: The interior of the material acts as an insulator, but its surface conducts electricity just as if it were coated with metal. Like the discovery of quasicrystals, these new materials forced scientists to rethink accepted views – in this case, that a material was either an insulator (in which electrons don’t move) or a conductor (in which electrons can easily flow). Since then, scientists have been searching for additional topological materials, both with a view to possible applications and to investigate their unique properties.
These three students asked themselves whether quasicrystals might have topological properties. A certain overlap among various studies hinted that the answer might, at least partly be positive: Topological materials and quasicrystals can both be described, in some sense, as “projections” of higher dimensional systems. Yet the models of quasicrystals they worked with did not reveal topological phenomena.
The first meeting of these two ideas occurred far from the Weizmann campus. Yoav and Oded ran into each other by chance on a fine Saturday afternoon in Tel Aviv. While chatting, the two realized that their respective research efforts could be complementary, and a meeting was soon set up between the theoretical group and the experimental one.
Working together, the five students succeeded in showing – in theoretical work and in experimental measurement – that quasicrystals do, indeed, have topological properties. In some ways these newly-discovered properties are similar to those of “regular” topological materials, but in other ways they are very different.
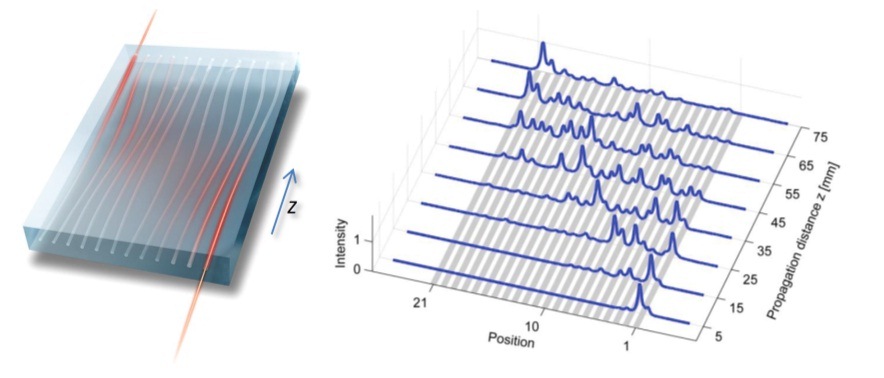
In experiments conducted in Silberberg’s lab, the students built a quasicrystal using an array of coupled thin optical fibers etched with a powerful laser beam into a single glass cube. The parallel fibers were arranged at quasiperiodic (non-repeating) distances. When light was shined into a central fiber in this system, it “hopped” to the other fibers, emerging from all the fibers at the other side. But when the light was introduced at one of the far edges of the array, it remained confined to that side. In other words, the quasicrystal setup showed an “edge state” with different properties than the states found in the middle of the array. Just as electrons in topological materials flow only on the surface and do not penetrate the interior, the light shined through the outer edge of the optical quasicrystal setup stayed in that plane. This finding was a surprise, as scientists had believed such topological behavior to be impossible in a one-dimensional system.
In an additional experiment, the team varied the distances between the optic fibers, so that they were no longer parallel along their entire length. When they got the arrangement just right, light going into a fiber at one edge hopped across the entire array, exiting from the fiber at the opposite edge. Though somewhat unexpected, this phenomenon, called an “adiabatic pump,” supplied further proof that the quasicrystal system had topological properties.
Adiabatic pumps are known from a different kind of topological system called a quantum Hall system, in which electrons are exposed to directional magnetic fields. The model the students developed to explain this behavior enabled them to envision the optical quasicrystal setup as a sort of one-dimensional cross section of a two-dimensional quantum Hall system. That cross section, to the team’s surprise, preserves the topological properties of the two-dimensional system. In other words, one-dimensional quasicrystals “inherit” their topological properties from higher-dimensional “ancestors,” which are periodic crystals.
These findings were recently published in Physical Review Letters, and they were highlighted in Science and other scientific journals. Now, among other things, the team is checking whether their results are applicable to other dimensions. For instance, the theory they developed suggests that topological properties in three-dimensional quasicrystals can be linked to topological systems existing in six dimensions.
Dr. Ehud Altman's research is supported by the Yeda-Sela Center for Basic Research; and the estate of Ernst and Anni Deutsch.
Prof.Yuval Gefen is the incumbent of the Isabelle and Samuel Friedman Professorial Chair of Theoretical Physics.
Prof. Yaron Silberberg's research is supported by the Crown Photonics Center, which he heads; the Cymerman - Jakubskind Prize; and the European Research Council. Prof. Silberberg is the incumbent of the Harry Weinrebe Professorial Chair of Laser Physics.
Share
