Are you a journalist? Please sign up here for our press releases
Subscribe to our monthly newsletter:
To design a multistory parking garage, you need to figure out how to pack the maximum number of cars into the smallest possible space while still allowing free passage between levels. Parking-garage-like structures in plant and animal cells evolved for similar purposes: Their thin, flat levels enable them to support large numbers of exposed molecules while continuous helical “ramps” connecting the layers facilitate the flow of various materials. In our cells, for example, they help create efficient assembly lines for protein production and folding; in plant cells, they house the complexes necessary for photosynthesis.
In parking garages, the architectural and engineering principles that guide the positioning of the helical ramps are permanently cast in concrete. Biological “parking garages,” however, are made of fluid membranes: embedded helical ramps can freely move around, repositioning themselves to optimize their elastic energy. Minute forces govern the arrangement of these biological structures, but to understand these springy structures, one must get an accurate description of their geometry. When Dr. Efi Efrati and postdoctoral fellow Dr. Luiz Da Silva of the Weizmann Institute of Science set out to do just that, they found that no appropriate mathematical tools existed, so they had to devise new ones.

Efrati is in the Physics of Complex Systems Department. His work spans a broad area connecting chemistry and the life sciences to physics and mathematics. Out of the entire range of physics – from elementary particles to the entire Universe – he has chosen to focus on the physics that takes place at the human scale: ranging from a few nanometers to a few meters. This field of study, called soft-matter physics, encompasses micron-wide lipid membranes and meter-wide soap films. Despite the differences in scale and chemical makeup, these both follow the same broad shaping principles and mathematical description. In particular, both systems form “minimal surfaces,” – surfaces of the smallest possible area that can span a given closed boundary. Minimal surfaces have been shown to minimize the surfaces’ bending energy, and they thus occur naturally in a variety of manmade and biological systems.
Embedded helical ramps can freely move around, repositioning themselves to optimize their elastic energy
Several years ago, Efrati began working with Prof. Ziv Reich of the Institute’s Biomolecular Sciences Department on garage-like structures called thylakoids, which are found in plant and green algal cells. Thylakoids house the photosynthetic complexes, and their structure lets them pack a lot of surface area – and hence lots of complexes – into a small space. In addition to their primary function – trapping light and using it to split water – thylakoids pump protons and facilitate the production of energy-storing molecules that emerge into the rest of the plant cell.
The electron microscopy reconstructions of thylakoids conducted in Reich’s group revealed that these organelles form minimal surfaces. They also found different embedded ramp structures, or “motifs,” that wound in different directions – some left- and others right-handed, each at a different slope, or pitch. Existing physical tools could describe the pitch of their slopes, but determining the spatial arrangement of the motifs, or understanding what determines their pitch ratio (that is, the slope compared to the diameter) required more delicate tools.
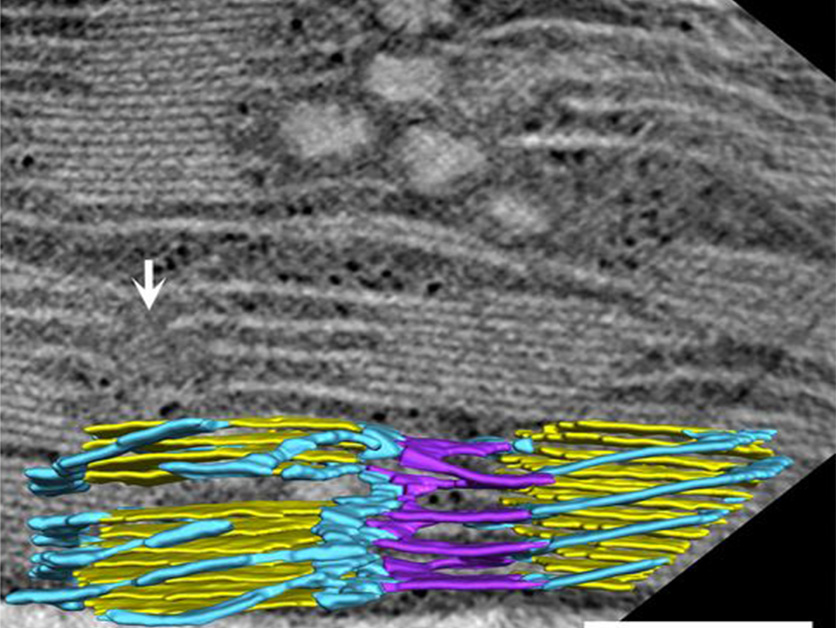
Minimal surfaces were discovered in the 18th century, and they are perhaps the most studied types of surfaces in the world of mathematics. Indeed, producing a minimal surface with one helical ramp follows a 250-year-old recipe. However, constructing a minimal surface that resembles the convoluted geometry of a thylakoid or the endoplasmic reticulum in our own cells is an entirely different story. “As physicists, we are exceptionally fond of approximations and idealization,” says Efrati. “We started with modeling the system using a common mathematical approximation to minimal surfaces.” This approximation allowed them to place the helical motifs at will and to construct arbitrarily complex parking-garage geometries, but the resulting structures were very far from being minimal surfaces. “We discovered that the approximation only applied when the motifs are very far apart. We had to find some way to produce an exact minimal surface.” Instead of starting from scratch, Da Silva and Efrati first tried to find a way to “amend” the approximation. “The approximation looked a lot like what we wanted, but with subtle differences, so we used it as a starting point for our calculation.” Da Silva and Efrati came up with a one-step “fix”: a distortion maneuver that considers the approximation for the entire surface and all its embedded helical ramps, and then calculates the lateral displacement for every point on the surface. The result is an exact minimal surface with the desired helical motifs embedded within. This allows an accurate construction of a minimal surface that has the complex geometry of the thylakoid structure.
The mathematical solution Efrati and Da Silva have created will give biological researchers the ability to conduct quantitative analyses of the physical organelles in cells. Because such parking-garage-like structures are found in many biological systems, this ability can further basic research, as well as that into disorders involving these structures; in the case of plants, it can foster improvements in their photosynthetic capabilities and energy management.