Spatiotemporal disorder
Weizmann Institute physicists studied pattern formation and spatiotemporal pattern dynamics in fluid systems. They discovered several scenarios of transition from ordered to disordered states in nonequilibrium hydrodynamical systems, and instabilities which are responsible for these transitions. In addition, they discovered a new type of spatiotemporal disorder called spiral and target chaos in Rayleigh-Benard convection in a gas near the gas-liquid critical point. They also found that a small addition of long polymer molecules has a strong influence on instability, pattern selection, and spatiotemporal dynamics in such systems.
Going with the flow
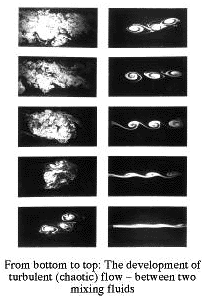
Turbulent, chaotic flow, one of the last, great, unresolved problems of statistical physics, is a universal phenomenon that occurs in gases and liquids traveling along a pipe, on the ground, or in open space. This phenomenon can be seen in daily life, for example, by turning on the tap in the kitchen and watching the water as it flows down the drain. At first it looks as if the water flows in an orderly fashion, but over time, and particularly when the force of the stream is increased, the flow becomes turbulent, agitated, chaotic. The flow of air around the body of a traveling car is also a turbulent flow, and it is one of the primary factors opposing the motion of the car and slowing it down.
So far, this phenomenon has not been fully understood, although there is a partial theory that manages to provide an approximate prediction of its development. Now Weizmann Institute scientists have devised a mathematical formulation that improves this existing theory's predictive ability, providing scientists with the building blocks needed to put together a final, exhaustive theory of chaotic, turbulent flow.
A comprehensive theory of turbulent flow should, for example, provide the necessary data to lessen the drag caused by resistant air currents around the bodies of cars and planes, significantly reducing their fuel consumption.
The behavior of flat whirlpools
A Weizmann Institute scientist developed a mathematical model of whirlpool behavior in a two-dimensional storm system, in liquid or gas. The two-dimensional model is useful in describing large whirlpools whose depth is negligible in relation to their area (and therefore are actually considered to be flat). Thus, for example, the model can predict the behavior of relatively thin dust clouds that disperse over thousands of kilometers, such as the cloud formations from very powerful volcanic eruptions.
In the past, various hypotheses were developed about the laws governing the turbulent mixing within whirlpools, but the Weizmann research provides the first mathematical description of these laws. In further studies, the scientists are now developing a model that can predict the eruption of chaotic jet streams from within volcanic clouds. These jet streams are capable of carrying contaminants to regions a great distance from the volcanic eruption.