Shaping the Future

 

 

 

In Israel's early years as a state, the Institute's mathematicians ran geophysical and seismological surveys designed to locate petroleum deposits. In 1955, this research led to the discovery of the first oil field in Israel. These studies provided the basis for the subsequent establishment of Israel's Institute for Petroleum Research and Geophysics, a government research corporation.

 

 

A seismologist from the Weizmann Institute installed and supervised the geophysical observatory near Eilat on the Red Sea, to monitor and distinguish between natural seismic activity and vibrations in the ground caused by human activity. Data were collected and analyzed about the seismic action of geological faults in the area, magnetic and acoustic activity in the atmosphere, and nuclear explosions. The data made it possible to analyze and chart seismic risk in Israel.

 

One result of the work was a theory that the seismic focus of every earthquake moves along a geological fault at high speed during the quake. This theory was subsequently confirmed.

 

In other research, data collected at the observatory on the experimental nuclear explosions carried out by the Soviet Union and China were compared with data about the mysterious explosion which took place at Tunguska, Siberia, in 1908. Based on this comparison, it was possible to calculate the energy of the explosion and the height above ground at which it occurred.

 

 

The fundamental laws of physics, chemistry, and engineering are clearly defined, but when they are applied to solving a variety of practical and theoretical problems, the calculations required are so complex that they cannot be carried out with complete accuracy.

 

In response, Weizmann Institute scientists developed numerous innovative approaches to the hierarchical organization of space-time, making these calculations far less complex. These approaches now help scientists to simplify calculations in the physics of elementary particles, medical imaging, radar analysis, astrophysics, weather forecasting, aerodynamic design, and oil prospecting. These new approaches should also provide scientists with a greater understanding of the architecture and interaction of chemical structures, which should in turn help in developing industrial materials and new drugs.

 

 

 

 

In contrast to the accepted view, there are goods for which demand goes up, not down, when their prices rise. This paradox, recognized for the past hundred or so years, is called the Giffen effect (named after the English economist Sir Robert Giffen, who lived at the end of the 19th century).

 

Mathematicians from the Weizmann Institute developed a mathematical model that outlines the conditions for the possible occurrence of phenomenon, after studying its existence in Japan. Based on a statistical analysis of domestic expenditure in Japan, the scientists discovered that demand for the inexpensive alcoholic drink shochu, which is particularly popular with low-income Japanese, increased when its price went up. This was because Japan's poor stopped buying more expensive drinks and spent their entire liquor budget on shochu.

 

The researchers developed a mathematical model that enables them to determine the degree of possible occurrence of the Giffen effect in a given economy. The model does not take into account the "snob appeal" associated with certain consumer products, nor of some consumers' tendency to prefer expensive goods because they assume they are of a higher quality than cheaper items.

 

 

Percolation is the process by which a liquid passes through pores in a nonhomogeneous, solid material. The mathematical models of percolation resemble models of magnetism and of phase transitions of matter. Consequently, gaining a more profound understanding of one of these processes contributes to a broader understanding of the others.

 

Weizmann Institute scientists developed two new mathematical models of percolation, which have many advantages over the previous models. Studies of the Weizmann scientists' original models led to the discovery of a new law connecting geometry of the solid matter (through which the liquid percolates) to the region which will be reached by the percolating liquid.

 

 

The notion of a "group" is very basic in mathematics. The group law is a binary operation, such as addition or multiplication of numbers, which can ultimately be used in the analysis of complex mathematical systems. Groups appear frequently in all areas of theoretical and applied mathematics as well as in computer science and other disciplines such as chemistry and physics.

 

The mathematical structure of groups (and of other similar systems) has been investigated as part of representation theory. In this theory, a second binary operation is introduced and their combined manipulation provides a very powerful tool in mathematics and in many of its applications. For example, they are used to describe elementary particles in physics. Indeed, certain representations enable physicists to predict the existence of particles which are subsequently discovered experimentally.

 

Mathematicians at the Weizmann Institute are attempting to solve some of the intricate open problems of representation theory and to uncover their deep connections to number theory, group theory, and ring theory.

 

 

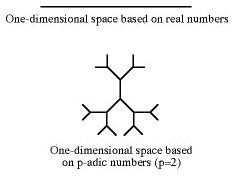
Geometry is usually described in coordinates of real numbers, with the differences between these numbers determining the geometric distance between different points in space. However, mathematicians are also aware of numbers with a different structure of distance between them. These numbers are known as p-adic numbers, and the distances between them are based on a mathematical relationship and prime numbers.

 

Is it possible to develop a geometry described in coordinates of p-adic numbers? Yes, according to Weizmann Institute scientists who showed, for example, that while a one-dimensional space based on real numbers is a simple line, one-dimensional space based on p-adic numbers is characterized by an infinitely branching structure.

 

 

 

Mathematics is used to describe processes in nature, and is also a design and control aid when human beings wish to harness the forces of nature. For example, mathematical principles are used when designing aircraft, power stations, irrigation systems and so on. Most quality-of-design inspections make use of computer imaging. Weizmann Institute scientists have made important contributions to the field of design and control mathematics.

 

Mathematical ideas developed by Weizmann scientists in the 1970s and 1980s are today applied to the design and inspection of aircraft stability, the stability of other advanced systems such as on board optical instruments, the stability and automatic repair of irrigation installations, and others.

 

Other research in this area focused on the optimal design of robot motion; for example, designing the path of a large robot in an area strewn with obstacles, and developing the ability to react to obstacles in the robot's path.

 

The Institute's scientists examined the stability of continuous processes, such as heat transition or undulant (wave-like) motion. Since these processes can create a continuum of disturbances and reactions, the scientists had to investigate and define the possible stable forms.

 

Further research in this field focuses on the design and control of interactions between bodies moving relatively slowly and processes taking place at high speed: for example, planning agriculture that can cope with frequent changes in the weather, or the motion of a car relative to the speed of its engine. In order to analyze such phenomena, Weizmann scientists developed a mathematical model which takes into account the differences between the various time scales of the processes.

 

A current topic of study is systems in which continuous processes are interwoven with discrete processes. The planning, monitoring and control of a continuous flow using a computer that operates digitally is one example of this.

 

The Institute's scientists are approaching these areas at a theoretical level, which integrates many fields of mathematics. Yet many of these ideas find their way into engineering textbooks and onto the desks of skilled engineers who apply them in a variety of areas.

 

 

Decisionmakers need good information to perform their role effectively. However, information may be an expensive product; if too much is demanded, it can turn a profitable process into one that will lose money. A mathematical model developed at the Weizmann Institute defines information as a decision-making variable which makes it possible to analyze the quantitative mutual interaction between information and the benefit it can bring, in situations in which optimal decisions must be taken against a background of uncertainty.

 

 

Many objects, from physical bodies to market indices, evolve or move along certain trajectories according to what are called differential equations, thus allowing for rigorous mathematical investigation. Weizmann Institute scientists are studying these trajectories from various viewpoints.

 

One of the projects focuses on a famous problem which has long posed a challenge to the international mathematical community. It was formulated in 1900 by David Hilbert, one of the world's most eminent mathematicians. He placed it at number sixteen on his famous list of twenty-or-so problems that mathematics of the 19th century bequeathed to the modern age.

 

The problem is to find the maximal possible number of cyclical, or periodic trajectories of planar motion, when the differential equation is defined by means of algebraic expressions. A complete solution is still a long way off, but the Institute's mathematicians have developed some new tools that allow for considerable advancement toward this goal. In particular, an almost complete solution has been found for equations that are small perturbations of energy-preserving cases.

 

 

 

 

 

When a planar body is rotated around a point within the body, it can immediately be seen that the collection of points common to all the rotations is a circle whose center is the point of rotation. It is easy to imagine that this phenomenon also applies in three dimensions, when the body common to all the rotations is a ball. It turns out that a similar phenomenon also holds true in spaces with higher numbers of dimensions.

 

The question is: How many rotations are needed to obtain a good approximation of the common ball? Mathematicians at the Weizmann Institute are investigating this complex mathematical problem, together with similar problems in the geometry of convex bodies of higher dimensions. The Institute's scientists discovered that the number of rotations needed depends very little on the body upon which the process is carried out.

 

The research is based on probabilistic considerations, and while it is impossible to indicate a particular way in which the requisite approximation will be obtained, it can be shown that there is a great probability of obtaining the approximation if the rotations are selected randomly.

 

 

Consider a collection of circles of different sizes in a plane, arranged so that they do not intersect. Some pairs of circles may touch each other and others will have no points of contact. Characterizing these relationships (known as tangencies) constitutes an interesting problem of combinatorics, related to other areas of mathematics and its applications.

 

Weizmann Institute mathematicians have made major contributions to this field of research, and have shown how to analyze instances where the packed bodies are not necessarily circles. This generalization has been found to have surprising implications in the theory of complex functions, which has many applications in physics.

 

 

 

 

 

In another research project, a Weizmann scientist proposed an explanation for an experiment carried out in the 1970s, in which balloons were sent into the atmosphere near the equator. Most of the balloons, as expected, stayed in the equatorial region, but a few of them traveled to the poles at a speed that could not be explained by the wind flow along the balloons' trajectories. In her proposed explanation, the Weizmann mathematician ascribed the reason for the deviation in the balloons' paths to resonance and chaotic motion, caused by a combination of the Earth's orbit rotation with the fact that the Earth's surface is not an exact sphere.

 

 

The sounds we hear are produced by vibrating objects, such as a string which alternately stretches and contracts. The frequency of the vibration determines how high a sound is produced. It has long been known that the frequencies of vibration depend on the composition and form of the vibrating material.

 

Similar predetermined rates appear in other areas of nature: For example, the energy levels of electrons in the atom, or the wavelengths that determine the color of light emitted by different materials. All of these phenomena share a common mathematical denominator: the frequencies are determined by the properties of certain models, such as matrices, and the way these models expand or contract the space on which they act. These stretching properties are determined by numerical coefficients called Eigen-values.

 

Weizmann Institute scientists have proposed a way to discover the properties of Eigen-values that correspond to high pitches, or high energy levels. This approach links the geometric and mechanical attributes of a material to its high frequencies. This research is important in understanding phenomena in a number of areas, such as mechanics, electronics, optics, and acoustics.